Understand recursion to understand recursion

We can imagine that any non-trivial program will at some stage have to loop over something and since we spoke of immutability in functional programming so much we might feel a bit hesitant to use our regular loops… Recursion comes to rescue, right?

What’s recursion, how does it actually work and how does it relate to immutability?

Recursion is a function that calls itself until an exit condition is met. It is a way to break down a large problem into smaller problems which when all solved will also solve the large problem. To put that into a real life perspective: drying my hair could be a form of a recursion. Dry my hair for a minute. Check if my hair is dry. If it’s dry, stop. Else, dry my hair for one minute.

How recursion works on stack

Before we jump into examples I would like to talk a little about stack as this is how recursion works internally. Let’s dig a little under the hood of a function call.

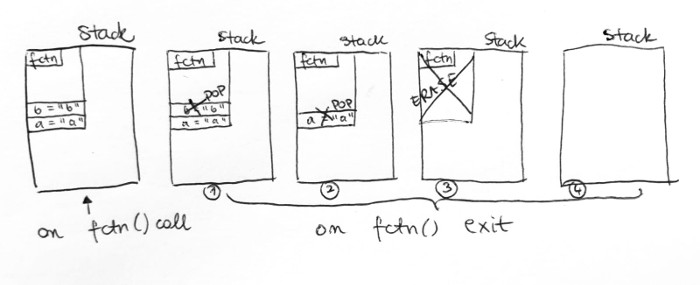
Stack is a place in memory where temporary variables created by function calls are stored. Stack is a last-in first-out (LIFO) data structure which means the last element added will be the first element removed. Anytime a function is called for the first time it creates a block in the stack where all of it’s arguments, any local variables it creates (and more) is pushed. Once the function exits, all elements on the stack are popped (last element pushed in will be first to be popped (LIFO)) and the block is erased. To visualise it:

 def fctn = {
    val a = "a"
    val b = "b"
 }

Given the above function this is want happens:

On fctn call:

1. Create a stack block for fctn
   
2. Push variable - a = "a"
   
3. Push variable - b = "b"
   

On fctn exit:

1. Pop variable (b)
   
2. Pop variable (a)
   
3. Erase fctn block
   

It’s a good time now to bring in a book classic recursive function: factorial.

 def factorial(n: Int): Int = {
    if(n <= 1) 1 // exit condition
    else n * factorial(n - 1) // recursive call to itself
 }

We can see this function consists of two parts:

• exit condition (a.k.a. base case)
• recursive call which will be called until exit condition is met

Now let’s see how factorial actually works when called. You see the recursive calls that go “down” (onto the stack) and return values that go “up” (off the stack) once calling function is evaluated (a bit simplified but that’s essentially how that works). As I mentioned before we can see here well how working out a smaller problem (factorial(1)) leads to working out the large problem (factorial(4)).

With the above explained it is easy to notice how important the exit condition is when it comes to recursion. If not for the exit condition above we would continue calling the factorial function infinitely.

Head recursion

Head recursion is a recursion that calls itself with an updated argument until the exit condition is met. A great example is our factorial function. As you can imagine the stack size is limited and therefore if we were to call factorial(1234) the code will throw StackOverflowException - there is no more space left on the stack for yet another call. This is something that we should avoid and so an alternative would be tail recursion.

Tail recursion

Tail recursion (if done right) is a way to avoid stack overflow exceptions. Tail recursive function is a function where the very last call is the call to itself. There is an accumulator that allows to pass a calculated value to the next recursive call as we go. In Scala they can be annotated with @tailrec.

So let’s rewrite our factorial:

 @tailrec
 def factorial(n: Int, accumulator: Int): Int =
    if(n <= 1) accumulator // exit condition
    else factorial(n - 1, n * accumulator) // recursive call to itself
 }

A couple of differences to head recursive version:

• Scala will allow you to annotate this code as tail recursion
• there is an accumulator
• there will be no “pyramid” of calls onto the stack like in head recursion because we are accumulating the calculated value as we go and pass it immediately on to the next recursive call.
  

The calls will look like this…

…which resembles a while loop a little bit…

PLOT TWIST! In Scala tail recursive functions are actually optimised to be while loops under the hood.

What.. So does recursion then help with sticking to immutability or not?

As each head recursive call is pushed onto a stack and then evaluated on function exit there is actually no mutation of variables, only function calls. It can cause stack overflow though, e.g. if we are getting a factorial of a large number so generally it is a better idea to write tail recursive functions. As I mentioned before in Scala they are actually automatically optimised to become while loops under the hood so *technically* tail recursion is not really a fully immutable solution.

So it comes down really to what would be your personal choice - recursion or a loop. I have quite a bit of confidence in Scala’s inner workings on optimization and so I go for tail recursive solutions. Apart from the Scala confidence part I find them more entertaining, generally more consistent with the rest of the codebase, looking more concise and I also don’t have to worry about bugs I could introduce while getting my own loops to work (like off-by-1 or so).

Real life

You can sure write a little factorial function or list some directories, but where could you possibly use recursion in real life and in real code?

This question bogged me quite a lot when starting my functional programming journey. I am a very hands-on engineer so I was skeptical when seeing Scala books talk of map, flatmap, fold and so on yet no mention on those recursive functions I was told I had to master. I just couldn’t see how to apply recursion in real programming, real problems.

It turns out there is two things nobody told me:

• most of the times you actually use transformation/aggregation methods like map, flatMap, foldLeft, foldRight, reduce, filter etc. instead of braining out recursion - check out this one liner implementation of our factorial function using foldLeft (which btw is implemented as tail recursion under the hood):
  

def factorial(i: Int) = (1 to i).toList.foldLeft(1)(_ * _)

…or reduce:

def factorial(i: Int) = (1 to i).toList.reduce(_ * _)

• realistically, you will need recursion for very custom problems - at work I actually had to write a number of recursive functions for nested Json containing a recursive data structure - there wasn’t a ready out-of-the-box solution like foldLeft on a list above.

I would like to stress the importance of writing tests for your recursive functions once you implement one - no matter how bulletproof the solution seems. I always test the happy path, the mean path but also the “this will never happen” path. With great power comes great responsibility and nothing makes you sleep at night as soundly as a well tested (especially recursive) code in production.

Summary

To summarize I would like to stress two rules of thumb for writing recursive functions:

• write your exit condition before writing anything else (here: if n <= 1)
• make sure you are moving towards the exit condition in your recursive calls (here: passing n - 1 to a recursive call - with each step moving closer towards1)

But remember - as a wise woman once said:

Where there is people practising recursion there stacks shall overflow and functions shall never exit.

I’ve been there and a lot of programmers have too. It’s difficult to get recursion right at first. But I promise if you commit to solving 30 problems recursively you will start seeing a new way of thinking emerging.

Recursion is a very helpful tool to have in your functional programming journey. Depending on what you’re working on you will likely not use it daily… probably not even monthly. But every now and then you will arrive at a custom problem that will beg to be solved recursively - and that’s when all your practice will pay off.

References:
Functional programming in Scala: Simplified by A. Alexander
Scala Cookbook by A. Alexander