What's functional programming?
Sooner or later every programmer comes across functional programming paradigm. Some of us get to work with it and some of us only hear about it, some of us maybe even try it out and can’t help but wonder - why is it so hype now? I was wondering this myself when I started. Functional programming at first can make little sense - in fact in a way it can even make you feel like it goes against what you’ve learnt before. If you’re anything like I was upon starting learning about it you could perhaps share a common enough misconception that you need to know maths very well first or that functional paradigm is a silver bullet to any programming problem.
In this post I will try to pinpoint a few basics that will allow you to understand what functional programming really is, what it is not, what it bases on, why people mention maths in its context so much, why you probably heard it’s difficult and why is it all over the news these days. Bear with me and I will try to cover all of those questions.
It’s all maths, right?
A very short answer to this question is: no.
A slightly longer answer to this question is: it’s a little bit closer to maths than imperative languages but it doesn’t mean you need to know maths inside out to write functional code. Will knowing certain branches of maths help? Yes. Is it crucial? No.
Think about a builder. Is it required of them to learn about the fundamentals of architecture and civil engineering? No. Would it benefit their understanding of why certain tasks have to be done a certain way even though it seems like an overkill? Very likely yes.
A long answer to this question is: functional programming bases on a branch of maths called category theory. In a MASSIVE oversimplification category theory is a branch of mathematics that reasons about categories and relationships between them instead of focusing on objects in categories, e.g. category theory would reason about negative numbers as an abstract idea rather than focusing on literal values like -2 or -23. Kinda like a bird’s eye view where you don’t see the details but patterns.
I am not gonna dive any deeper as this could easily be a topic for a separate blog altogether - but let’s agree the main take away from category theory should be composability - assembling smaller functions* into larger functions. You will see this everywhere in functional programming. Let’s talk about it a little:
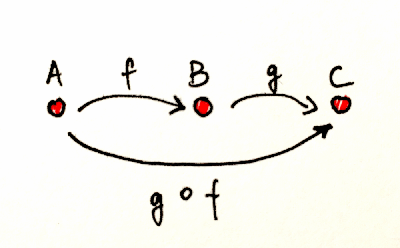
Considering above image - if f is a function that goes from A to B and g is a function that goes from B to C then there must be a composition like g o f which goes from A to C.
In Scala terms (a very cumbersome way of getting length of numbers that shows composability):
val A = List(1, 11, 111)
def f: Int => String = _.toString
def g: String => Int = _.length
def gof: Int => Int = g compose f // g and f composed
A.map(gof) // List(1, 2, 3)Let’s rewrite the above statement to match our Scala example:
if f is a function that goes from Int to String and g is a function that goes from String to Int then there must be a composition like g o f which goes from Int to Int.
Another way of imagining composability is good ould piping of shell commands (below example actually resembles a real program flow already). Each function below can be composed of smaller functions:
get_data_command | verify_data_command | process_data_command > output.data.fileWhat’s functional programming then?
When I think functional programming I think algebra - you evaluate functions and compose them until you get what you need. You stay away from side effects and don’t mutate data. And as there is no mutation and no side effects the results are always deterministic. And if the results are always deterministic there is no need to worry about hidden state changes. And if you don’t have to worry about hidden state changes then you can parallelise execution. And if you can parallelise execution that means happy days with multi threading. And that all comes down to using powerful multi core CPUs which are pretty much a standard nowadays.
Let’s understand the algebra part - I believe that’s one of the reasons why maths is mentioned a lot in the context of functional programming.
Back in the days in your maths classes while doing algebra it would be obvious that z was at all times going to evaluate to 8:
x = 5
y = 3
z = x + yMutating wouldn’t be allowed and so imagine what your teacher would have to say about something like this:
x = 5
x = 3
y = 3
z = x + y…does it not resemble imperative ways a little?
var number = 5
number = 3
var number2 = 3
println(number + number2) // 6Now the example above with mutated number doesn’t seem like the end of the world but try and imagine what would happen if number = 3 was actually called by another function, on another thread perhaps. And that function would take its time. Our result wouldn’t actually be 6 but 8 even though once the code is executed number would be 3. Now to put that to a perspective imagine number and number2 aren’t integers but actual objects that update customer data…
Functional programming steps away from mutability to avoid those issues (all examples from now on will be in Scala):
val number = 3 // val is immutable
number = 5 // error: reassignment to val
But if you can’t mutate anything then how do you even program?
It’s a good time to bring pure functions to the table. A pure function is a function that has no side effects. A pure function takes an input value and without modifying it does some calculation and returns something new. Pure functions are composable, deterministic, have no side effects and therefore can be parallelised which goes back to my previous points.
Two rules of thumb that will help you with never mutating yet udpating are:
- update as you copy
- use val only and never var
This shows best with Scala’s case classes.
case class User(id: String, name: String)
val user = User("123", "annette")
// pure function, update as you copy:
def updateUser(user: User, newName: String) = user.copy(name = newName)
val newUser = updateUser(user, "john")
println(newUser) // User(123,john)As case classes are immutable by default it wouldn’t even be possible to write an impure update function that would compile.
But if you can’t mutate then what about for loops?
When it comes to Scala the true answer is that it depends on how much of a functional purist you want to be. I can already imagine a huge debate on the topic of using mutable data in local unexposed functions and whether or not it’s a bad practice. Myself, I prefer to stick to immutability which means that I don’t use for loops, but instead I map or use recursion - this makes my code nice, pure and it feels consistent. Also, there is something quite satisfying about seeing that perfect recursive function pass all the test cases…
If everything is pure and immutable how do you design your program?
This was a very important question that I was stuck with for quite some time as there is clear differences yet obviously there is no golden rule. There is books written on this topic but the general rule of thumb I noticed is to separate data from functions as much as possible. Think about the composition image I showed above. It could look something like:
case class A // only data
case class B // only data
case class C // only data
def f: A => B = ??? // only function
def g: B => C = ??? // only function
def gof: A => C = ??? // only functionSummary
With all the above information let’s try and fight a few misconceptions that I mentioned in the beginning of the post.
Misconception 1: Functional programming is all about maths.
It depends how deep you want to dig. It derives from category theory but you don’t need to be a maths guru at all to learn functional programming. As long as you know your algebrae :)
Misconception 2: Functional programming is a silver bullet.
There is no silver bullet in programming. Functional programming just as any other paradigm is just a tool in your toolbox - it won’t be a best choice for all tasks. Sure you can hit a nail with a crowbar but other tools might simply be more suitable.
Misconception 3: Functional programming is difficult.
It’s a different way of thinking which makes it appear more complex. It’s obviously not a rule but I personally find that sometimes things that are considered very easy the imperative ways tend to seem a bit more complicated or cumbersome in functional programming. It’s all a matter of practice and with time you get to “rewire” your ways of thinking. But even once you have your brain rewired I can guarantee that the learning will never cease, be it functional or any other paradigm!
*I deliberately skipped correct category theory terminology to avoid confusion. To clarify: correct terminology is “morphisms”, not “functions”.
References:
Category theory for programmers by B. Milewski
Basic Category Theory by T. Leinster
Scala Cookbook by A. Alexander
Credits:
M. Bagnicka - thanks for your help with polishing my builder analogy :)